test20191016

发表于

题面

题面

$T1$

Solution

首先，我们需要明确一个事实：对每一段 $0/1$ 能填的数是固定的。

画图证明一下。

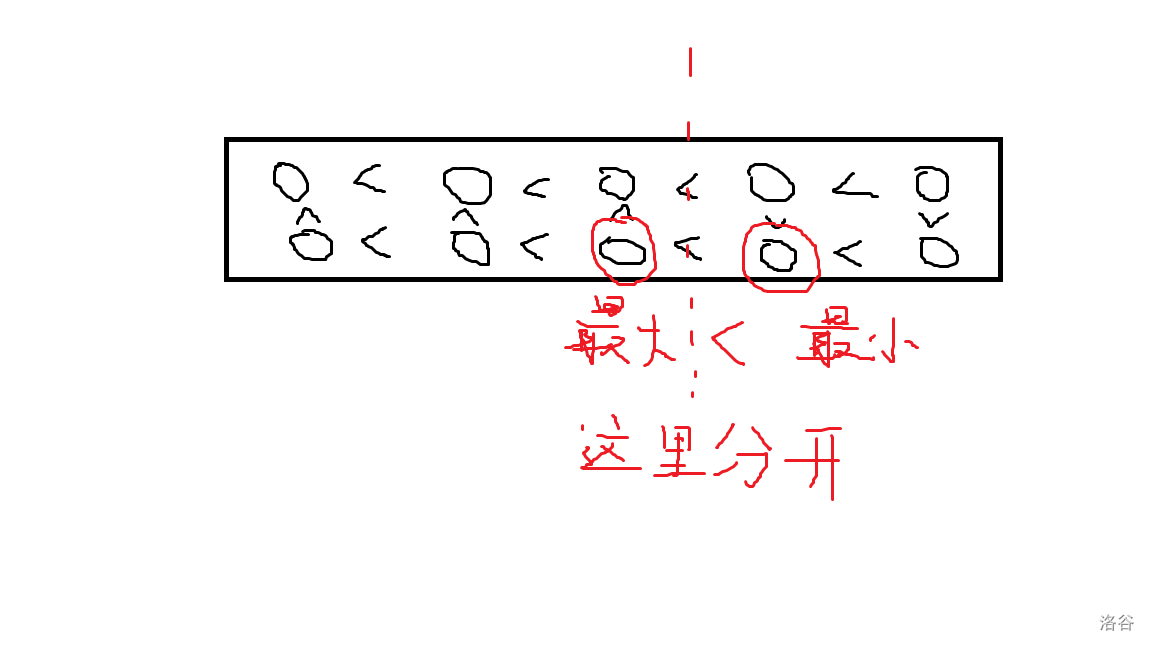
可以看出后面一段的最小值大于前面一段的最大值。然后对于所有的段，我们从后往前填入，可以发现，刚好是连续的一段。

所以我们只需要分开找出每一段的答案，再乘起来就行了。

通过打表或者构造双射的方法，我们可以发现答案就是 $Catalan$ 数，然后就可以$O(n)$ 解决了。

$Catalan$ 数

计算公式：

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
#include<bits/stdc++.h>
#define del(a,i) memset(a,i,sizeof(a))
#define ll long long
#define inl inline
#define il inl void
#define it inl int
#define ill inl ll
#define re register
#define ri re int
#define rl re ll
#define mid ((l+r)>>1)
#define lowbit(x) (x&(-x))
#define INF 0x3f3f3f3f
using namespace std;
template<class T>il read(T &x){
	int f=1;char k=getchar();x=0;
	for(;k>'9'||k<'0';k=getchar()) if(k=='-') f=-1;
	for(;k>='0'&&k<='9';k=getchar()) x=(x<<3)+(x<<1)+k-'0';
	x*=f;
}
template<class T>il _print(T x){
	if(x/10) _print(x/10);
	putchar(x%10+'0');
}
template<class T>il print(T x){
	if(x<0) putchar('-'),x=-x;
	_print(x);
}
ll mul(ll a,ll b,ll mod){long double c=1.;return (a*b-(ll)(c*a*b/mod)*mod)%mod;}
it qpow(int x,int m,int mod){
	int res=1,bas=x%mod;
	while(m){
		if(m&1) res=(1ll*res*bas)%mod;
		bas=(1ll*bas*bas)%mod,m>>=1;
	}
	return res%mod;
}
const int MAXN = 2e5+5,mod = 998244353;
int n,val[MAXN],ans=1,fac[MAXN],inv[MAXN],ifac[MAXN];
char s[MAXN];
it add(int x,int y){return x+y>=mod?x+y-mod:x+y;}
it mul(int x,int y){return 1ll*x*y%mod;}
it C(int n,int m){return mul(fac[n],mul(ifac[m],ifac[n-m]));}
it catalan(int x){return add(C(x<<1,x),mod-C(x<<1,x-1));}
int main(){
//	freopen(".in","r",stdin);
//	freopen(".out","w",stdout);
	read(n),scanf("%s",s+1),s[n+1]='a';
	fac[0]=ifac[0]=1;
	for(ri i=1;i<=(n<<1);++i) fac[i]=mul(fac[i-1],i);
	ifac[n<<1]=qpow(fac[n<<1],mod-2,mod);
	for(ri i=(n<<1)-1;i;--i) ifac[i]=mul(ifac[i+1],i+1);
	for(ri i=1,cnt=1;i<=n;++i){
		if(s[i]!=s[i+1]) ans=mul(ans,catalan(cnt)),cnt=1;
		else ++cnt;
	}
	print(ans);
	return 0;
}

$T2$

Solution